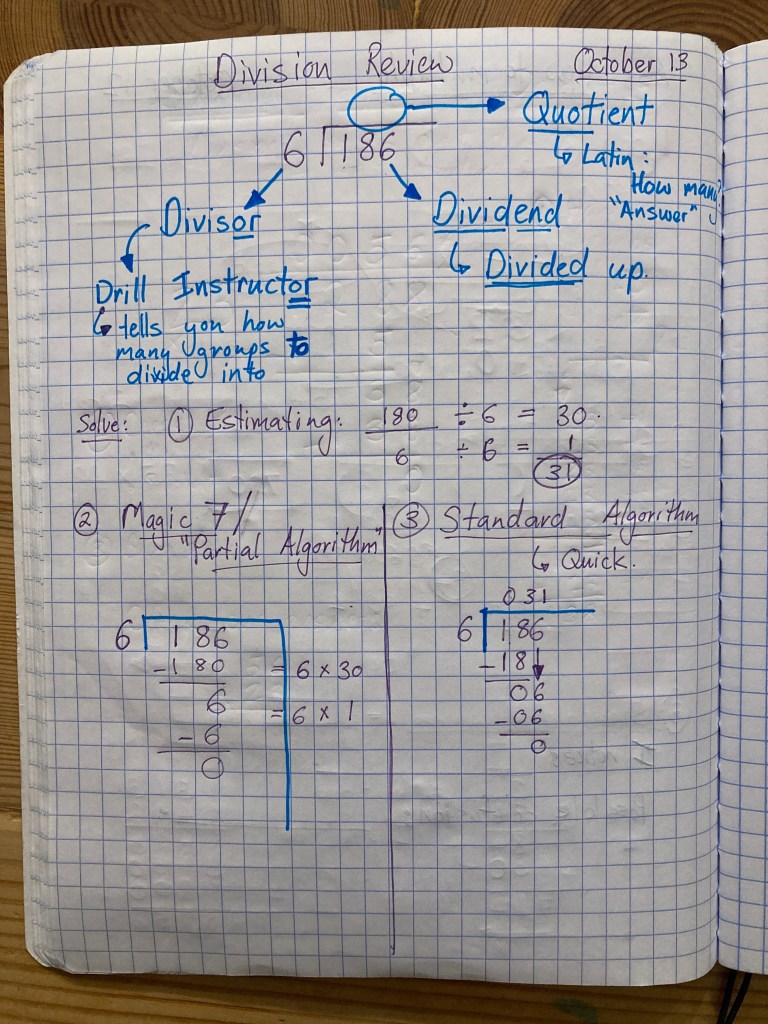
The second part of Unit 6 is understanding how to use the standard algorithm for division in word problems. We begin by reviewing our division vocabulary and connecting estimation and the partial algorithm (“magic 7”) to the standard algorithm.
In our mini-lesson today, we dived into the steps of using the standard algorithm for multiplication. We reviewed how to multiply each level and explored why this shortcut works (it takes advantage of place value). We also spent time reflecting on what we noticed in the algorithm and areas of possible confusion. We also did a lot of these!
We learned about variables, expressions, and equations in class today and how they can be used to represent multiplication.
Today we’re on to another topic already! Unit 6 focuses on learning the standard algorithm (or shortcut) for multiplication and division. We then use those skills in real-world problems.
Our lesson today recaps our objectives, how estimating helps in multiplication, and how the partial algorithm (“box method”) connects to the standard algorithm.
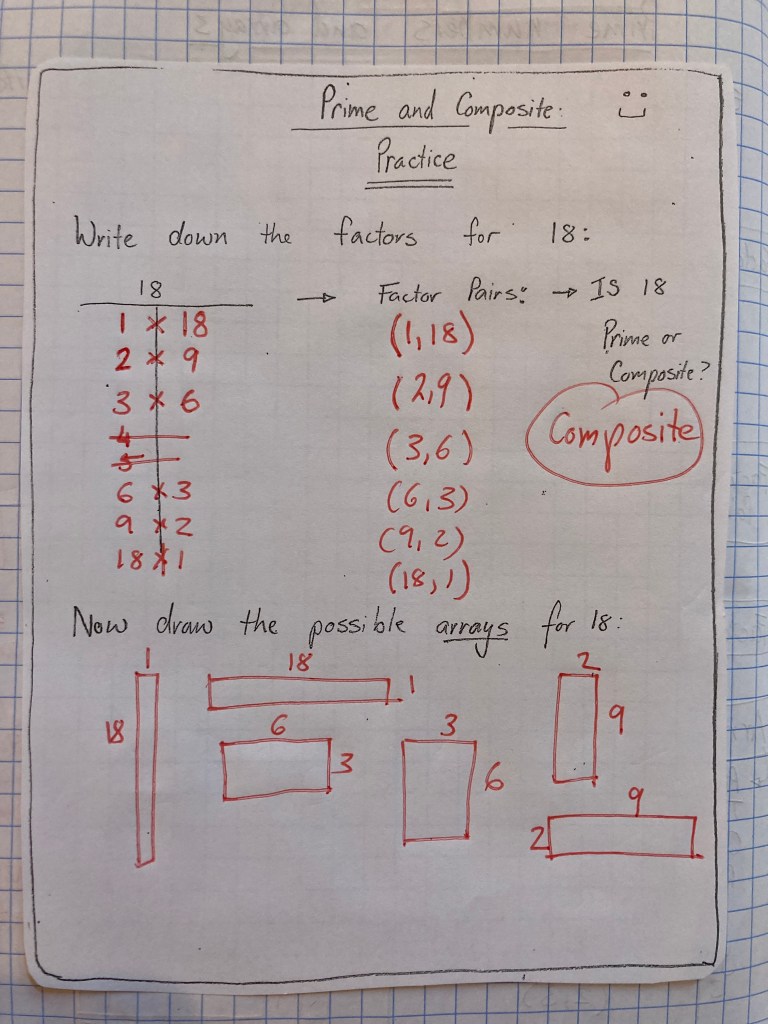
Today we continued learning about prime and composite numbers and how they can be represented visually in arrays. We noticed the interesting phenomenon that prime numbers can be represented by two arrays (think a table with rows and columns) where each array has only one column or one row! Composite numbers have more array configurations.
Our lesson today reviewed the concepts of factors (numbers which are multiplied together to give a product) and multiples (think skip counting, or where a number is multiplied by 1, 2, 3 … and so on). We saw how multiples are infinite but factors are a defined set and limited for a particular number. Factors also come in pairs: 4 x 9 are factors of 36 because they multiply together to give the product 36. We reviewed how factors and multiples are important for fractions, prime, and composite numbers.
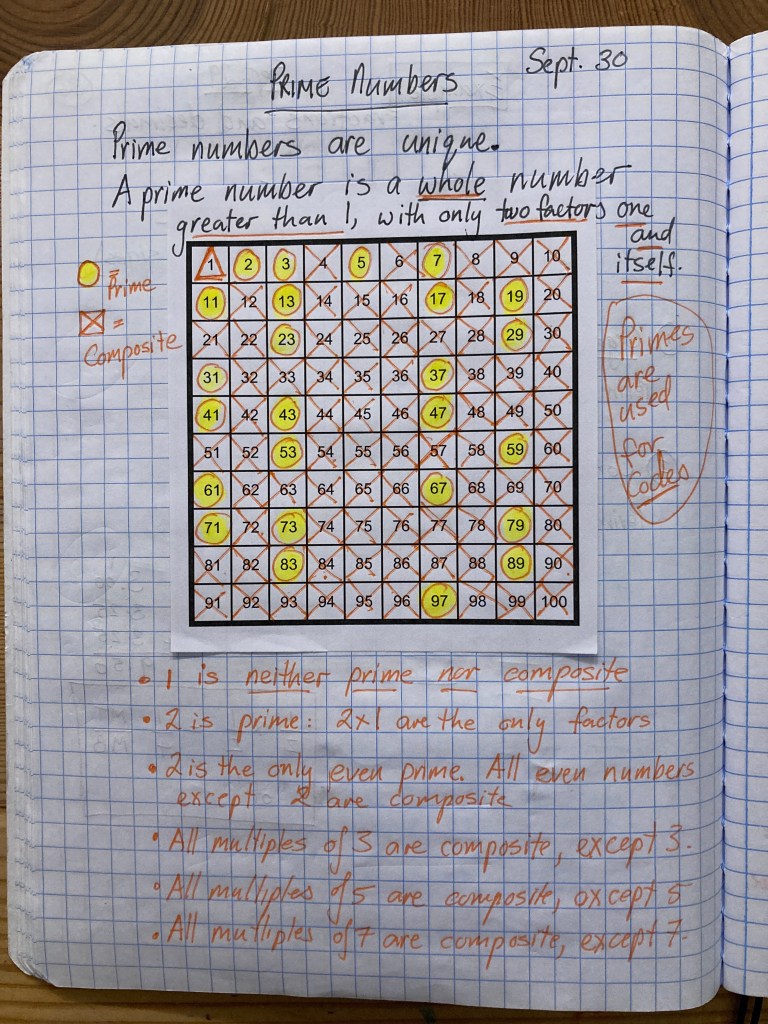
Today we start Unit 5, focusing on the unique (and sometimes mysterious-:) numbers known as prime and composite numbers. We learned that prime numbers have only two factors: the number itself and one. Another way of describing a prime number is that it can be divide equally only by itself and one. A composite number (“composed” or made up of prime numbers) has more than two factors. We investigated the patterns of primes up to 100 and previewed how prime numbers shape math and other fields.
Today the lesson portion of class focused on working through examples with both decimals and fractions. In discussion, we also previewed how to multiply fractions and reviewed area and perimeter.
Students in class today asked about benchmark fractions such as 1/3 and how they would convert to decimals. As they noticed, the issue is that 1 cannot be equally divided by three, so we can use a recurring (or repeating) decimal as an approximation.
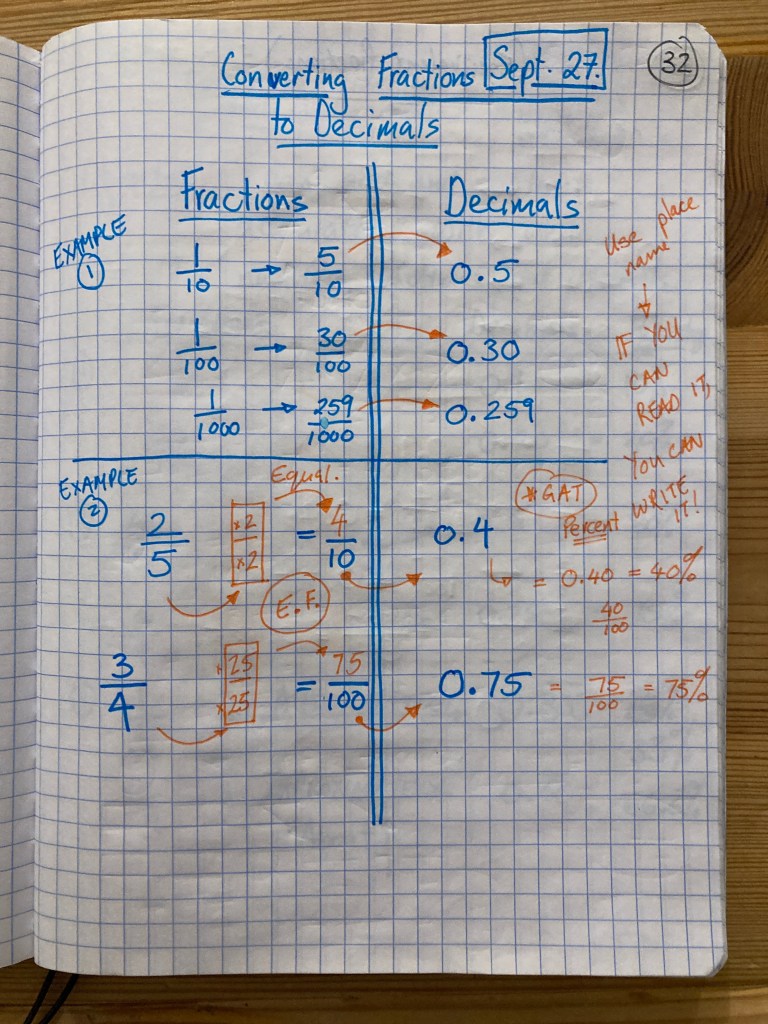
Our lesson today examines how to convert fractions to decimals where the fraction does not have a denominator which is a multiple of ten. As you can guess, the step we follow is to convert that fraction first to an equivalent fraction with a denominator of ten (or a multiple of ten). From there, it is easy to convert to decimals.
Mr. J’s Math Class